Printed from www.flong.com/texts/code/shapers_poly/
Contents © 2020 Golan Levin and Collaborators
Golan Levin and Collaborators
Code
- Peer-Reviewed Publications
- Essays and Statements
- Interviews and Dialogues
- Catalogues and Lists
- Project Reports
- Press Clippings
- Lectures
- Code
- Misc.
- 07 2006. Shaping Functions: Polynomial
- 07 2006. Shaping Functions: Exponential
- 07 2006. Shaping Functions: Circular and Elliptical
- 07 2006. Shaping Functions: Bezier and Parametric
Polynomial Shaping Functions
This page presents a collection of polynomial functions for shaping, tweening, and easing signals in the range [0...1]. Functions include:
- Blinn-Wyvill Approximation to the Raised Inverted Cosine
- Double-Cubic Seat
- Double-Cubic Seat with Linear Blend
- Double-Odd-Polynomial Seat
- Symmetric Double-Polynomial Sigmoids
- Quadratic Through a Given Point
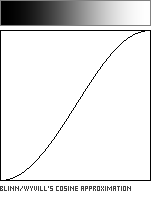
Blinn-Wyvill Approximation to the Raised Inverted Cosine
Trigonometric functions like cos() and sin() are ubiquitous in natural sciences, engineering and animation, but they can be expensive to compute. If a situation calls for millions of trigonometric operations per second, substantial speed optimizations can be obtained by using an approximation constructed from simple arithmetic functions. An example is the Blinn-Wyvill polynomial approximation to the Raised Inverted Cosine, which diverges from the authentic (scaled) trigonometric function by less than 0.1% within the range [0...1]. It also shares some of the Raised Inverted Cosine's key properties, having flat derivatives at 0 and 1, and the value 0.5 at x=0.5. It has the strong advantage that it is relatively efficient to compute, since it is comprised exclusively from simple arithmetic operations and cacheable fractions. Unlike the Raised Inverted Cosine, it does not have infinite derivatives, but since it is a sixth-order function, this limitation is unlikely to be noticed in practice.
This would be a useful approximation for the cos() and sin() trigonometric functions for a small microprocessor (such as an Arduino) which has limited speed and math capabilities.
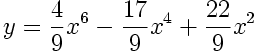
//---------------------------------------------
float blinnWyvillCosineApproximation (float x){
float x2 = x*x;
float x4 = x2*x2;
float x6 = x4*x2;
final float fa = ( 4.0/9.0);
final float fb = (17.0/9.0);
final float fc = (22.0/9.0);
float y = fa*x6 - fb*x4 + fc*x2;
return y;
}
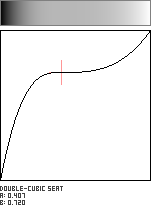
Double-Cubic Seat
This seat-shaped function is formed by joining two 3rd-order polynomial (cubic) curves. The curves meet with a horizontal inflection point at the control coordinate (a,b) in the unit square.
![]()
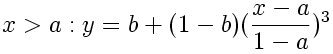
//------------------------------------------------
float doubleCubicSeat (float x, float a, float b){
float epsilon = 0.00001;
float min_param_a = 0.0 + epsilon;
float max_param_a = 1.0 - epsilon;
float min_param_b = 0.0;
float max_param_b = 1.0;
a = min(max_param_a, max(min_param_a, a));
b = min(max_param_b, max(min_param_b, b));
float y = 0;
if (x <= a){
y = b - b*pow(1-x/a, 3.0);
} else {
y = b + (1-b)*pow((x-a)/(1-a), 3.0);
}
return y;
}
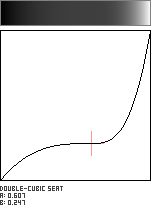
Double-Cubic Seat with Linear Blend
This modified version of the Double-Cubic Seat function uses a single variable to control the location of its inflection point along the diagonal of the unit square. A second parameter is used to blend this curve with the Identity Function (y=x). Here, we use the variable b to control the amount of this blend, which has the effect of tilting the slope of the curve's plateau in the vicinity of its inflection point. The adjustable flattening around the inflection point makes this a useful shaping function for lensing or magnifying evenly-spaced data.
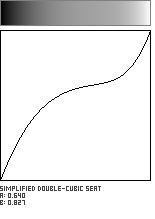
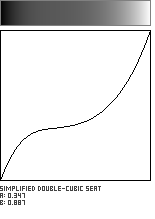
![]()
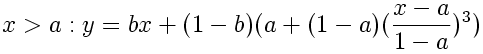
//---------------------------------------------------------------
float doubleCubicSeatWithLinearBlend (float x, float a, float b){
float epsilon = 0.00001;
float min_param_a = 0.0 + epsilon;
float max_param_a = 1.0 - epsilon;
float min_param_b = 0.0;
float max_param_b = 1.0;
a = min(max_param_a, max(min_param_a, a));
b = min(max_param_b, max(min_param_b, b));
b = 1.0 - b; //reverse for intelligibility.
float y = 0;
if (x<=a){
y = b*x + (1-b)*a*(1-pow(1-x/a, 3.0));
} else {
y = b*x + (1-b)*(a + (1-a)*pow((x-a)/(1-a), 3.0));
}
return y;
}
Double-Odd-Polynomial Seat
The previous Double-Cubic Seat function can be generalized to a form which uses any odd integer exponent. In the code below, the parameter n controls the flatness or breadth of the plateau region in the vicinity of the point (a,b). A good working range for n is the set of whole numbers from 1 to about 20.
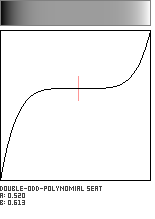
![]()

//---------------------------------------------------------------
float doubleOddPolynomialSeat (float x, float a, float b, int n){
float epsilon = 0.00001;
float min_param_a = 0.0 + epsilon;
float max_param_a = 1.0 - epsilon;
float min_param_b = 0.0;
float max_param_b = 1.0;
a = min(max_param_a, max(min_param_a, a));
b = min(max_param_b, max(min_param_b, b));
int p = 2*n + 1;
float y = 0;
if (x <= a){
y = b - b*pow(1-x/a, p);
} else {
y = b + (1-b)*pow((x-a)/(1-a), p);
}
return y;
}
Odd-powered polynomials, such as cubics and quintics, lend themselves very naturally to creating seat-shaped curves. This example is parametrically blended with the Identity Function (y=x), as regulated by the parameter a; the shaping function passes through the corners of the unit square (0,0) and (1,1) and symmetrically through the midpoint (0.5, 0.5). It is also relatively efficient to compute.
![]()
Symmetric Double-Polynomial Sigmoids
It is possible to generate sigmoid patterns by joining a symmetric pair of polynomials at the center of the unit square. The exponents in these equations (controlled by the integer parameter n) control the steepness of the wall separating the squelched values from the boosted ones; a suggested range for the whole number n is from 1 to about 10. Of these, the sigmoid created with a 2nd-order (quadratic) exponent comes closest to the Raised Inverted Cosine, approximating it to within 2.8%.
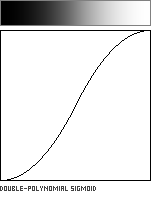
The Symmetric Double-Polynomial Sigmoids presented here create an S-shape with flat tangents at 0 and 1, and with the special property that f(0.5) = 0.5. Sigmoids generated with even exponents require the following equations:
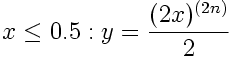

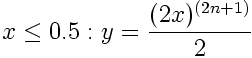
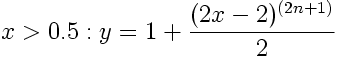
//---------------------------------------------------------------
float doublePolynomialSigmoid (float x, float a, float b, int n){
float y = 0;
if (n%2 == 0){
// even polynomial
if (x<=0.5){
y = pow(2.0*x, n)/2.0;
} else {
y = 1.0 - pow(2*(x-1), n)/2.0;
}
}
else {
// odd polynomial
if (x<=0.5){
y = pow(2.0*x, n)/2.0;
} else {
y = 1.0 + pow(2.0*(x-1), n)/2.0;
}
}
return y;
}
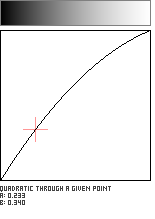
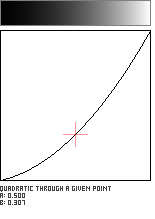
Quadratic Through a Given Point
This function defines an axis-aligned quadratic (parabola) which passes through a user-supplied point (a,b) in the unit square. Caution: Not all points in the unit square will produce curves which pass through the locations (0,0) and (1,1).
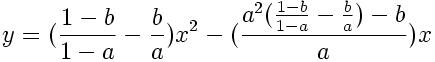
//------------------------------------------------------------
float quadraticThroughAGivenPoint (float x, float a, float b){
float epsilon = 0.00001;
float min_param_a = 0.0 + epsilon;
float max_param_a = 1.0 - epsilon;
float min_param_b = 0.0;
float max_param_b = 1.0;
a = min(max_param_a, max(min_param_a, a));
b = min(max_param_b, max(min_param_b, b));
float A = (1-b)/(1-a) - (b/a);
float B = (A*(a*a)-b)/a;
float y = A*(x*x) - B*(x);
y = min(1,max(0,y));
return y;
}