Flong

Printed from www.flong.com/texts/code/shapers_circ/
Contents © 2020 Golan Levin and Collaborators

Golan Levin and Collaborators

Code

Circular & Elliptical Shaping Functions

  • Circular Interpolation: Ease-In and Ease-Out 
  • Double-Circle Seat
  • Double-Circle Sigmoid
  • Double-Elliptic Seat
  • Double-Elliptic Sigmoid
  • Double-Linear with Circular Fillet
  • Circular Arc Through a Given Point

Circular Interpolation: Ease-In and Ease-Out

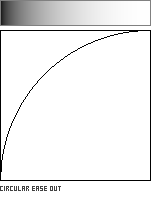
A circular arc offers a quick and easy-to-code method for easing in or out of the unit square. The computational efficiency of the function is diminished by its use of a square root, however.


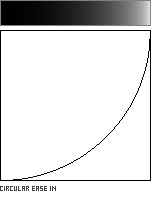
Ease-In interpolation:

Ease-Out interpolation: 

//------------------------------
float circularEaseIn (float x){
  float y = 1 - sqrt(1 - x*x);
  return y;
}

//------------------------------
float circularEaseOut (float x){
  float y = sqrt(1 - sq(1 - x));
  return y;
}

Double-Circle Seat

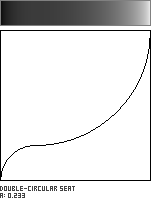
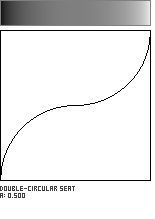
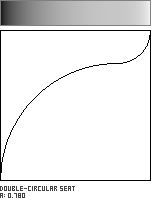
This shaping function is formed by the meeting of two circular arcs, which join with a horizontal tangent. The parameter a, in the range [0...1], governs the location of the curve's inflection point along the diagonal of the unit square.


//----------------------------------------
float doubleCircleSeat (float x, float a){
  float min_param_a = 0.0;
  float max_param_a = 1.0;
  a = max(min_param_a, min(max_param_a, a)); 

  float y = 0;
  if (x<=a){
    y = sqrt(sq(a) - sq(x-a));
  } else {
    y = 1 - sqrt(sq(1-a) - sq(x-a));
  }
  return y;
}

Double-Circle Sigmoid

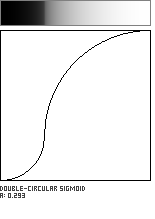
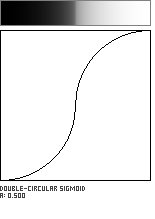
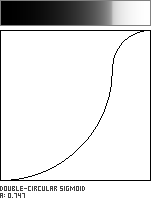
This sigmoidal shaping function is formed by the meeting of two circular arcs, which join with a vertical tangent. The parameter a, in the range [0...1], governs the location of the curve's inflection point along the diagonal of the unit square.


//-------------------------------------------
float doubleCircleSigmoid (float x, float a){
  float min_param_a = 0.0;
  float max_param_a = 1.0;
  a = max(min_param_a, min(max_param_a, a)); 

  float y = 0;
  if (x<=a){
    y = a - sqrt(a*a - x*x);
  } else {
    y = a + sqrt(sq(1-a) - sq(x-1));
  }
  return y;
}

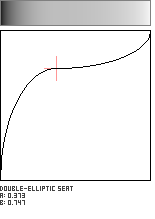
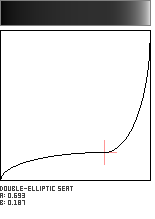
Double-Elliptic Seat

This seat-shaped function is created by the joining of two elliptical arcs, and is a generalization of the Double-Circle Seat. The two arcs meet at the coordinate (a,b) with a horizontal tangent.


//---------------------------------------------------
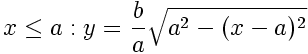
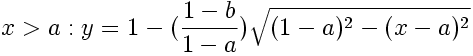
float doubleEllipticSeat (float x, float a, float b){
  float epsilon = 0.00001;
  float min_param_a = 0.0 + epsilon;
  float max_param_a = 1.0 - epsilon;
  float min_param_b = 0.0;
  float max_param_b = 1.0;
  a = max(min_param_a, min(max_param_a, a)); 
  b = max(min_param_b, min(max_param_b, b)); 

  float y = 0;
  if (x<=a){
    y = (b/a) * sqrt(sq(a) - sq(x-a));
  } else {
    y = 1- ((1-b)/(1-a))*sqrt(sq(1-a) - sq(x-a));
  }
  return y;
}

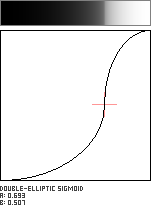
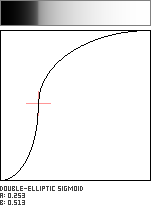
Double-Elliptic Sigmoid

This sigmoid-shaped function is created by the joining of two elliptical arcs, and is a generalization of the Double-Circle Sigmoid. The arcs meet at the coordinate (a, b) in the unit square with a vertical tangent.

 

//------------------------------------------------------
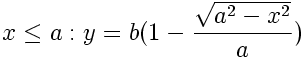
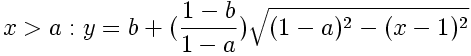
float doubleEllipticSigmoid (float x, float a, float b){

  float epsilon = 0.00001;
  float min_param_a = 0.0 + epsilon;
  float max_param_a = 1.0 - epsilon;
  float min_param_b = 0.0;
  float max_param_b = 1.0;
  a = max(min_param_a, min(max_param_a, a)); 
  b = max(min_param_b, min(max_param_b, b));
 
  float y = 0;
  if (x<=a){
    y = b * (1 - (sqrt(sq(a) - sq(x))/a));
  } else {
    y = b + ((1-b)/(1-a))*sqrt(sq(1-a) - sq(x-1));
  }
  return y;
}

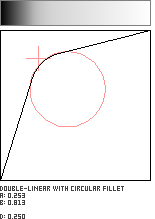
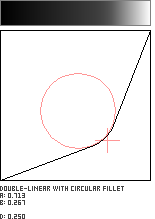
Double-Linear with Circular Fillet

This pattern joins two straight lines with a circular arc whose radius is adjustable. The user specifies the fillet's radius (with parameter c) and the coordinate in the unit square where the lines would otherwise intersect (with parameters a and b). This pattern is adapted from Robert D. Miller's "Joining Two Lines with a Circular Arc Fillet", which appears in Graphics Gems III.

//--------------------------------------------------------
// Joining Two Lines with a Circular Arc Fillet
// Adapted from Robert D. Miller / Graphics Gems III.

float arcStartAngle;
float arcEndAngle;
float arcStartX,  arcStartY;
float arcEndX,    arcEndY;
float arcCenterX, arcCenterY;
float arcRadius;

//--------------------------------------------------------
float circularFillet (float x, float a, float b, float R){
  
  float epsilon = 0.00001;
  float min_param_a = 0.0 + epsilon;
  float max_param_a = 1.0 - epsilon;
  float min_param_b = 0.0 + epsilon;
  float max_param_b = 1.0 - epsilon;
  a = max(min_param_a, min(max_param_a, a)); 
  b = max(min_param_b, min(max_param_b, b)); 

  computeFilletParameters (0,0, a,b, a,b, 1,1,  R);
  float t = 0;
  float y = 0;
  x = max(0, min(1, x));
  
  if (x <= arcStartX){
    t = x / arcStartX;
    y = t * arcStartY;
  } else if (x >= arcEndX){
    t = (x - arcEndX)/(1 - arcEndX);
    y = arcEndY + t*(1 - arcEndY);
  } else {
    if (x >= arcCenterX){
      y = arcCenterY - sqrt(sq(arcRadius) - sq(x-arcCenterX)); 
    } else{
      y = arcCenterY + sqrt(sq(arcRadius) - sq(x-arcCenterX)); 
    }
  }
  return y;
}

//------------------------------------------
// Return signed distance from line Ax + By + C = 0 to point P.
float linetopoint (float a, float b, float c, float ptx, float pty){
  float lp = 0.0;
  float d = sqrt((a*a)+(b*b));
  if (d != 0.0){
    lp = (a*ptx + b*pty + c)/d;
  }
  return lp;
}

//------------------------------------------
// Compute the parameters of a circular arc 
// fillet between lines L1 (p1 to p2) and
// L2 (p3 to p4) with radius R.  
// 
void computeFilletParameters (
  float p1x, float p1y, 
  float p2x, float p2y, 
  float p3x, float p3y, 
  float p4x, float p4y,
  float r){

  float c1   = p2x*p1y - p1x*p2y;
  float a1   = p2y-p1y;
  float b1   = p1x-p2x;
  float c2   = p4x*p3y - p3x*p4y;
  float a2   = p4y-p3y;
  float b2   = p3x-p4x;
  if ((a1*b2) == (a2*b1)){  /* Parallel or coincident lines */
    return;
  }

  float d1, d2;
  float mPx, mPy;
  mPx = (p3x + p4x)/2.0;
  mPy = (p3y + p4y)/2.0;
  d1 = linetopoint(a1,b1,c1,mPx,mPy);  /* Find distance p1p2 to p3 */
  if (d1 == 0.0) {
    return; 
  }
  mPx = (p1x + p2x)/2.0;
  mPy = (p1y + p2y)/2.0;
  d2 = linetopoint(a2,b2,c2,mPx,mPy);  /* Find distance p3p4 to p2 */
  if (d2 == 0.0) {
    return; 
  }

  float c1p, c2p, d;
  float rr = r;
  if (d1 <= 0.0) {
    rr= -rr;
  }
  c1p = c1 - rr*sqrt((a1*a1)+(b1*b1));  /* Line parallel l1 at d */
  rr = r;
  if (d2 <= 0.0){
    rr = -rr;
  }
  c2p = c2 - rr*sqrt((a2*a2)+(b2*b2));  /* Line parallel l2 at d */
  d = (a1*b2)-(a2*b1);

  float pCx = (c2p*b1-c1p*b2)/d; /* Intersect constructed lines */
  float pCy = (c1p*a2-c2p*a1)/d; /* to find center of arc */
  float pAx = 0;
  float pAy = 0;
  float pBx = 0;
  float pBy = 0;
  float dP,cP;

  dP = (a1*a1) + (b1*b1);        /* Clip or extend lines as required */
  if (dP != 0.0){
    cP = a1*pCy - b1*pCx;
    pAx = (-a1*c1 - b1*cP)/dP;
    pAy = ( a1*cP - b1*c1)/dP;
  }
  dP = (a2*a2) + (b2*b2);
  if (dP != 0.0){
    cP = a2*pCy - b2*pCx;
    pBx = (-a2*c2 - b2*cP)/dP;
    pBy = ( a2*cP - b2*c2)/dP;
  }

  float gv1x = pAx-pCx; 
  float gv1y = pAy-pCy;
  float gv2x = pBx-pCx; 
  float gv2y = pBy-pCy;

  float arcStart = (float) atan2(gv1y,gv1x); 
  float arcAngle = 0.0;
  float dd = (float) sqrt(((gv1x*gv1x)+(gv1y*gv1y)) * ((gv2x*gv2x)+(gv2y*gv2y)));
  if (dd != (float) 0.0){
    arcAngle = (acos((gv1x*gv2x + gv1y*gv2y)/dd));
  } 
  float crossProduct = (gv1x*gv2y - gv2x*gv1y);
  if (crossProduct < 0.0){ 
    arcStart -= arcAngle;
  }

  float arc1 = arcStart;
  float arc2 = arcStart + arcAngle;
  if (crossProduct < 0.0){
    arc1 = arcStart + arcAngle;
    arc2 = arcStart;
  }

  arcCenterX    = pCx;
  arcCenterY    = pCy;
  arcStartAngle = arc1;
  arcEndAngle   = arc2;
  arcRadius     = r;
  arcStartX     = arcCenterX + arcRadius*cos(arcStartAngle);
  arcStartY     = arcCenterY + arcRadius*sin(arcStartAngle);
  arcEndX       = arcCenterX + arcRadius*cos(arcEndAngle);
  arcEndY       = arcCenterY + arcRadius*sin(arcEndAngle);
}

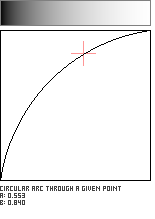
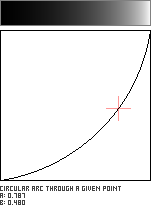
Circular Arc Through a Given Point

This function defines a circular arc which passes through a user-specified point in the unit square. Unfortunately, not every location in the unit square lends itself to defining a circle which also is confined to the unit square; the user-supplied point must inhabit a zone close to the main (Identity) diagonal. This pattern is adapted from Paul Bourke's Equation of a Circle From 3 Points. 

//---------------------------------------------------------
// Adapted from Paul Bourke 
float m_Centerx;
float m_Centery;
float m_dRadius;

float circularArcThroughAPoint (float x, float a, float b){  
  float epsilon = 0.00001;
  float min_param_a = 0.0 + epsilon;
  float max_param_a = 1.0 - epsilon;
  float min_param_b = 0.0 + epsilon;
  float max_param_b = 1.0 - epsilon;
  a = min(max_param_a, max(min_param_a, a));
  b = min(max_param_b, max(min_param_b, b));
  x = min(1.0-epsilon, max(0.0+epsilon, x));
  
  float pt1x = 0;
  float pt1y = 0;
  float pt2x = a;
  float pt2y = b;
  float pt3x = 1;
  float pt3y = 1;

  if      (!IsPerpendicular(pt1x,pt1y, pt2x,pt2y, pt3x,pt3y))		
     calcCircleFrom3Points (pt1x,pt1y, pt2x,pt2y, pt3x,pt3y);	
  else if (!IsPerpendicular(pt1x,pt1y, pt3x,pt3y, pt2x,pt2y))		
     calcCircleFrom3Points (pt1x,pt1y, pt3x,pt3y, pt2x,pt2y);	
  else if (!IsPerpendicular(pt2x,pt2y, pt1x,pt1y, pt3x,pt3y))		
     calcCircleFrom3Points (pt2x,pt2y, pt1x,pt1y, pt3x,pt3y);	
  else if (!IsPerpendicular(pt2x,pt2y, pt3x,pt3y, pt1x,pt1y))		
     calcCircleFrom3Points (pt2x,pt2y, pt3x,pt3y, pt1x,pt1y);	
  else if (!IsPerpendicular(pt3x,pt3y, pt2x,pt2y, pt1x,pt1y))		
     calcCircleFrom3Points (pt3x,pt3y, pt2x,pt2y, pt1x,pt1y);	
  else if (!IsPerpendicular(pt3x,pt3y, pt1x,pt1y, pt2x,pt2y))		
     calcCircleFrom3Points (pt3x,pt3y, pt1x,pt1y, pt2x,pt2y);	
  else { 
    return 0;
  }

  // constrain
  if ((m_Centerx > 0) && (m_Centerx < 1)){
     if (a < m_Centerx){
       m_Centerx = 1;
       m_Centery = 0;
       m_dRadius = 1;
     } else {
       m_Centerx = 0;
       m_Centery = 1;
       m_dRadius = 1;
     }
  }
  
  float y = 0;
  if (x >= m_Centerx){
    y = m_Centery - sqrt(sq(m_dRadius) - sq(x-m_Centerx)); 
  } else {
    y = m_Centery + sqrt(sq(m_dRadius) - sq(x-m_Centerx)); 
  }
  return y;
}

//----------------------
boolean IsPerpendicular(
float pt1x, float pt1y,
float pt2x, float pt2y,
float pt3x, float pt3y)
{
  // Check the given point are perpendicular to x or y axis 
  float yDelta_a = pt2y - pt1y;
  float xDelta_a = pt2x - pt1x;
  float yDelta_b = pt3y - pt2y;
  float xDelta_b = pt3x - pt2x;
  float epsilon = 0.000001;

  // checking whether the line of the two pts are vertical
  if (abs(xDelta_a) <= epsilon && abs(yDelta_b) <= epsilon){
    return false;
  }
  if (abs(yDelta_a) <= epsilon){
    return true;
  }
  else if (abs(yDelta_b) <= epsilon){
    return true;
  }
  else if (abs(xDelta_a)<= epsilon){
    return true;
  }
  else if (abs(xDelta_b)<= epsilon){
    return true;
  }
  else return false;
}

//--------------------------
void calcCircleFrom3Points (
float pt1x, float pt1y,
float pt2x, float pt2y,
float pt3x, float pt3y)
{
  float yDelta_a = pt2y - pt1y;
  float xDelta_a = pt2x - pt1x;
  float yDelta_b = pt3y - pt2y;
  float xDelta_b = pt3x - pt2x;
  float epsilon = 0.000001;

  if (abs(xDelta_a) <= epsilon && abs(yDelta_b) <= epsilon){
    m_Centerx = 0.5*(pt2x + pt3x);
    m_Centery = 0.5*(pt1y + pt2y);
    m_dRadius = sqrt(sq(m_Centerx-pt1x) + sq(m_Centery-pt1y));
    return;
  }

  // IsPerpendicular() assure that xDelta(s) are not zero
  float aSlope = yDelta_a / xDelta_a; 
  float bSlope = yDelta_b / xDelta_b;
  if (abs(aSlope-bSlope) <= epsilon){	
    // checking whether the given points are colinear. 	
    return;
  }

  // calc center
  m_Centerx = (
     aSlope*bSlope*(pt1y - pt3y) + 
     bSlope*(pt1x + pt2x) - 
     aSlope*(pt2x+pt3x) )
     /(2* (bSlope-aSlope) );
  m_Centery = -1*(m_Centerx - (pt1x+pt2x)/2)/aSlope +  (pt1y+pt2y)/2;
  m_dRadius = sqrt(sq(m_Centerx-pt1x) + sq(m_Centery-pt1y));
}